Contact Dynamics Predictions Utilizing theNESC Parameterless Contact Model

December 19, 2024

Read Time:2 Minute

Download PDF: Contact Dynamics Predictions Utilizing theNESC Parameterless Contact Model

Modeling the capture of the Mars Sample Return (MSR) Orbiting Sample (OS) involves understanding complex dynamic behavior, which includes the OS making contact against the interior of the capture enclosure. The MSR Program required numerical verification of the contact dynamics’ predictions produced using their commercial software tools. This commercial software used “free” parameters to set up the contact modeling. Free parameters (also known as free variables) are not based on contact physics. The commercial contact model used by MSR
required seven free parameters including a Hertzian contact stiffness, surface penetration, stiffening exponent, penetration velocity, contact damping, maximum penetration depth for the contact damping value, and a smoothing function. An example of a parameter that is not free is coefficient of friction, which is a physics-based parameter. Consider the free parameter, contact stiffness. Contact stiffness is already present in the finite element model’s (FEM) stiffness matrix where the bodies come into contact, and surface penetration is disallowed in a physically realizable contact model, as FEM meshes should not penetrate one another during contact (i.e., the zero-contact limit penetration constraint condition).

As such, with each set of selected free parameters generating a different contact force signature, additional numerical verification is required to guide setting these parameters. Contact modeling is nonlinear. This means that the stiffness matrices of contacting bodies are continuously updated as the bodies come into contact, potentially recontact (due to vibrations), and disengage. The modal properties of contacting bodies continuously change with state transitions (e.g., stick-to-slip). Some contact models have been proposed and incorporated in commercial finite element analysis solvers, and most involve static loading. A relatively smaller number involve dynamics, which has historically proven challenging.

IT NESC f1-contact-force-and-relative-displacement-

In 2005, NASA conducted a study testing several commercial contact solvers in predicting contact forces in transient dynamic environments. This was necessitated by the Space Shuttle Program (SSP)—after the February 2003 Columbia accident— deciding to include contact dynamics in the Space Shuttle transient coupled loads analysis (CLA) to capture the impact of contact nonlinearities. This rendered the entire CLA nonlinear. The study found major difficulties executing nonlinear CLAs in commercial software. A nonlinear solver developed by the NESC and Applied Structural Dynamics (ASD) that was able to produce physically realizable results was numerically verified by NASA and later experimentally validated as well. This nonlinear solver was subsequently utilized to execute all NASA SSP CLAs (i.e., crewed space flights) from 2005 to the final flight in 2011, as well as currently supporting the SLS Program.

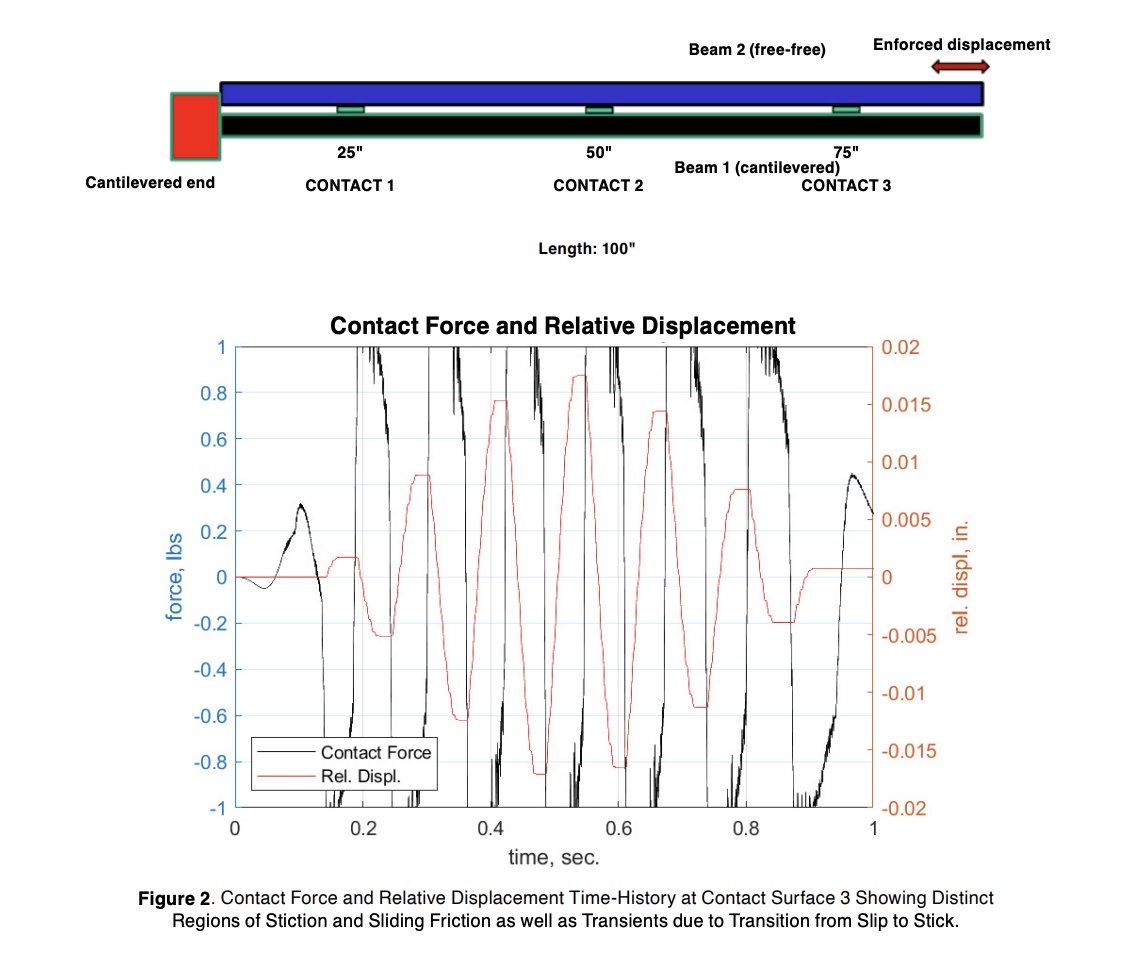
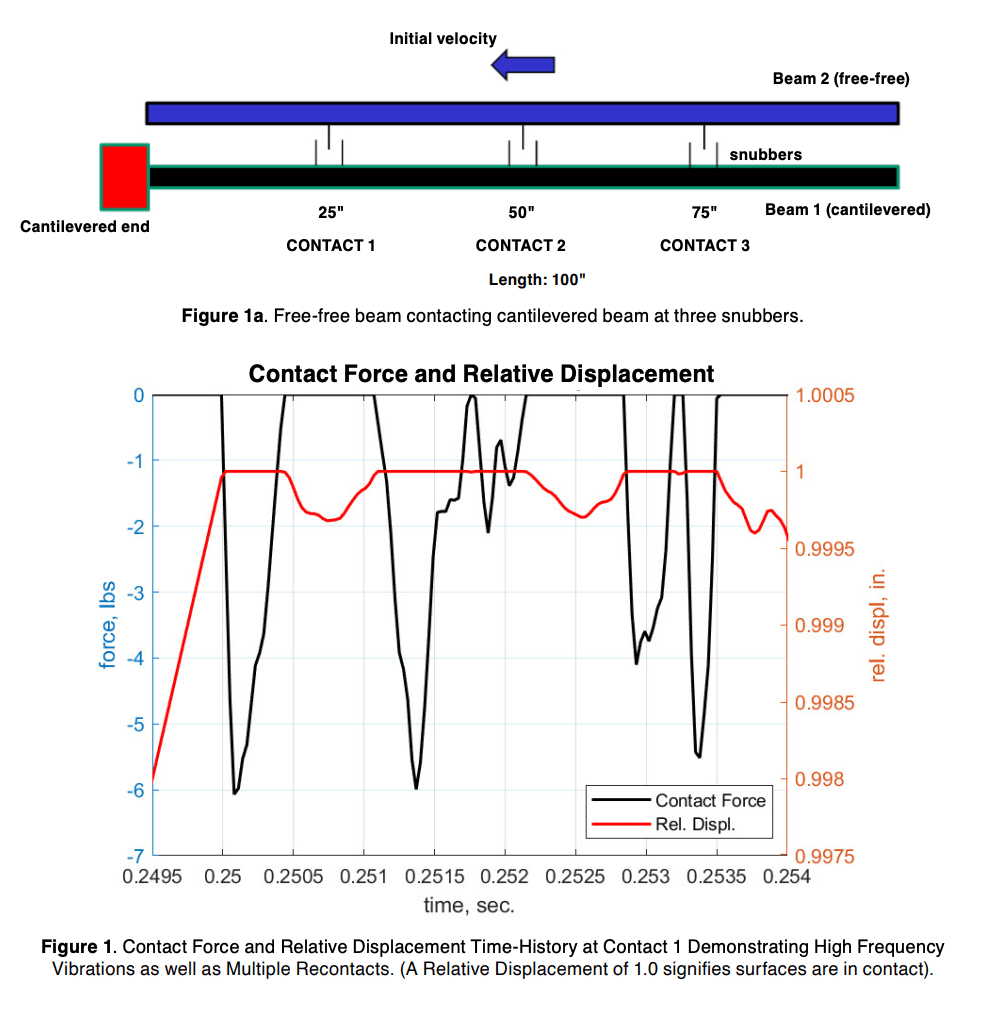
The objective of the MSR contact verification work was to provide data that could be used by the MSR team to help define the free parameters listed above for the commercial tool contact model. The NESC/ASD solver was used to model contact between simple cantilever and free beams, deriving contact forces and relative displacements. These resulting data can be used to determine parameter values for more complex structures. Two of the modeled configurations, one for axial contact (Figure 1) and the other for stick/friction (Figure 2), and sample results from the NESC nonlinear dynamic analyses are presented in Figures 1 and 2.